In machine learning, after collecting data, cleaning data, and designing preprocessing algorithms, how do we know the effectiveness of the algorithm? How to evaluate whether the predictive model can classify effectively and how accurate the classification is? This involves the confusion matrix, which is widely used to evaluate classification problems in machine learning (mainly supervised learning). This article will cover the following parts:
- What is a confusion matrix
- Calculation of confusion matrix in binary classification problems
What is a Confusion Matrix
In classification problems, the evaluation of machine learning algorithms involves four concepts:
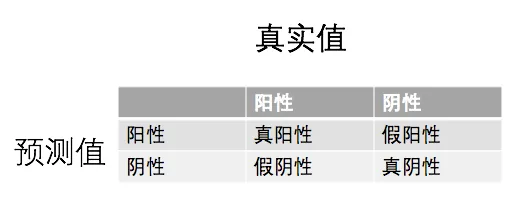
(1) If an instance is positive and is predicted as positive, it is a True Positive (TP)
(2) If an instance is positive but is predicted as negative, it is a False Negative (FN)
(3) If an instance is negative but is predicted as positive, it is a False Positive (FP)
(4) If an instance is negative and is predicted as negative, it is a True Negative (TN)
As shown in the table below:
Below is a specific explanation assuming a pregnancy test example.
True Positive:
You predict or detect positive, and the detection result is accurate.
That means your test result shows a woman is pregnant, and the actual result is that she really is pregnant.
True Negative:
The predicted result shows negative but the actual result is positive.
The test shows the woman is not pregnant, but the actual result is that she is pregnant.
False Positive (Type I error):
The predicted result shows positive but the actual result is negative.
In this example, a man is tested as pregnant, but the actual situation is that he is not pregnant.
False Negative (Type II error):
The predicted result shows negative but the actual situation is positive.
In this example, a woman is tested as not pregnant, but the actual situation is that she is pregnant.
In summary, the judgment method is first to predict whether it is positive or negative, then check the truth value of the prediction.
- If predicted positive and prediction is correct, it is True Positive.
- If predicted positive but prediction is wrong, it is False Positive.
- If predicted negative and prediction is correct, it is True Negative.
- If predicted negative but prediction is wrong, it is False Negative.
Calculation of Confusion Matrix in Binary Classification Problems
After understanding the confusion matrix content, next is to calculate various parameters, mainly recall, precision, and accuracy.
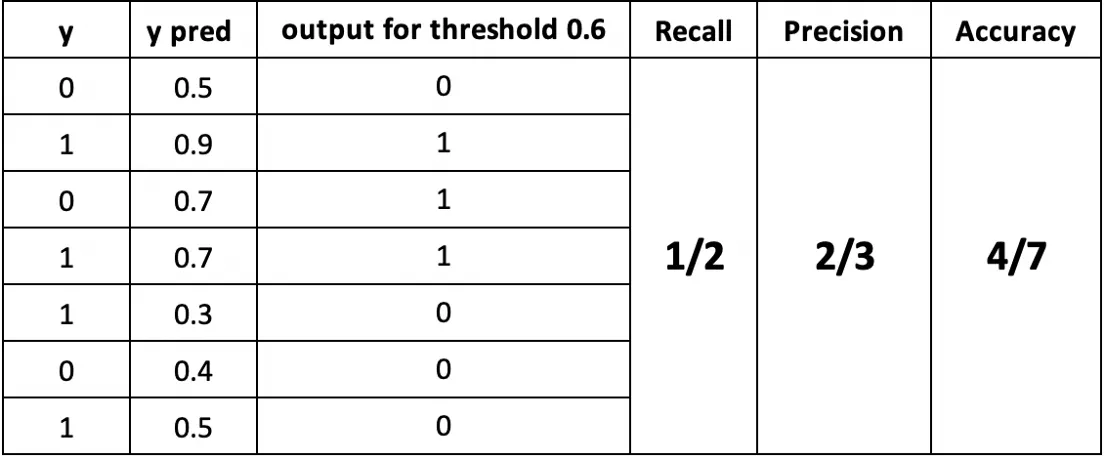
Recall Calculation
recall = TP / (TP + FN)
This describes the proportion of samples predicted as positive among all samples that are actually positive. By definition, the higher the recall, the better.
In the example, samples 2, 4, 5, and 7 are truly positive. Predictions show samples 2 and 4 as positive, so recall is 2/4 = 1/2.
Precision Calculation
precision = TP / (TP + FP)
This describes the proportion of truly positive samples among all samples predicted as positive. The higher, the better.
In the example, three samples (2, 3, and 4) are predicted as positive, and samples 2 and 4 are truly positive, so precision is 2/3.
Accuracy Calculation
accuracy = (TP + TN) / (TP + FP + TN + FN)
This describes the proportion of correctly classified samples among all samples. Of course, the higher the better.
In the example, there are 7 samples in total, with samples 1, 2, 4, and 6 correctly classified, so accuracy is 4/7.
In practice, when two algorithms have inconsistent recall and precision performance, how do we compare their quality? Here is an extensively used metric called f-measure.
f-measure Calculation
The f-measure, or F-score:
f_measure = 2 * recall * precision / (recall + precision)
The F-score considers both recall and precision, and can be used to compare the performance of different algorithms.
Summary
This article introduced the confusion matrix used in machine learning to evaluate model quality, explained its concepts, and how to calculate various model parameters in practical situations.
