Python Implementation of Classic Sorting Algorithms (1)

In computer science, a sorting algorithm is an algorithm that arranges a list of data in a specific order. The most commonly used sorting methods are numerical order and lexicographical (dictionary) order. Efficient sorting algorithms are crucial in various other algorithms. Sorting algorithms are also used in processing text data and generating human-readable output.

Basically, the output of a sorting algorithm must adhere to the following two principles:

1. The output result is an increasing sequence (increasing refers to the desired sort order).
2. The output result is a permutation or rearrangement of the original input.

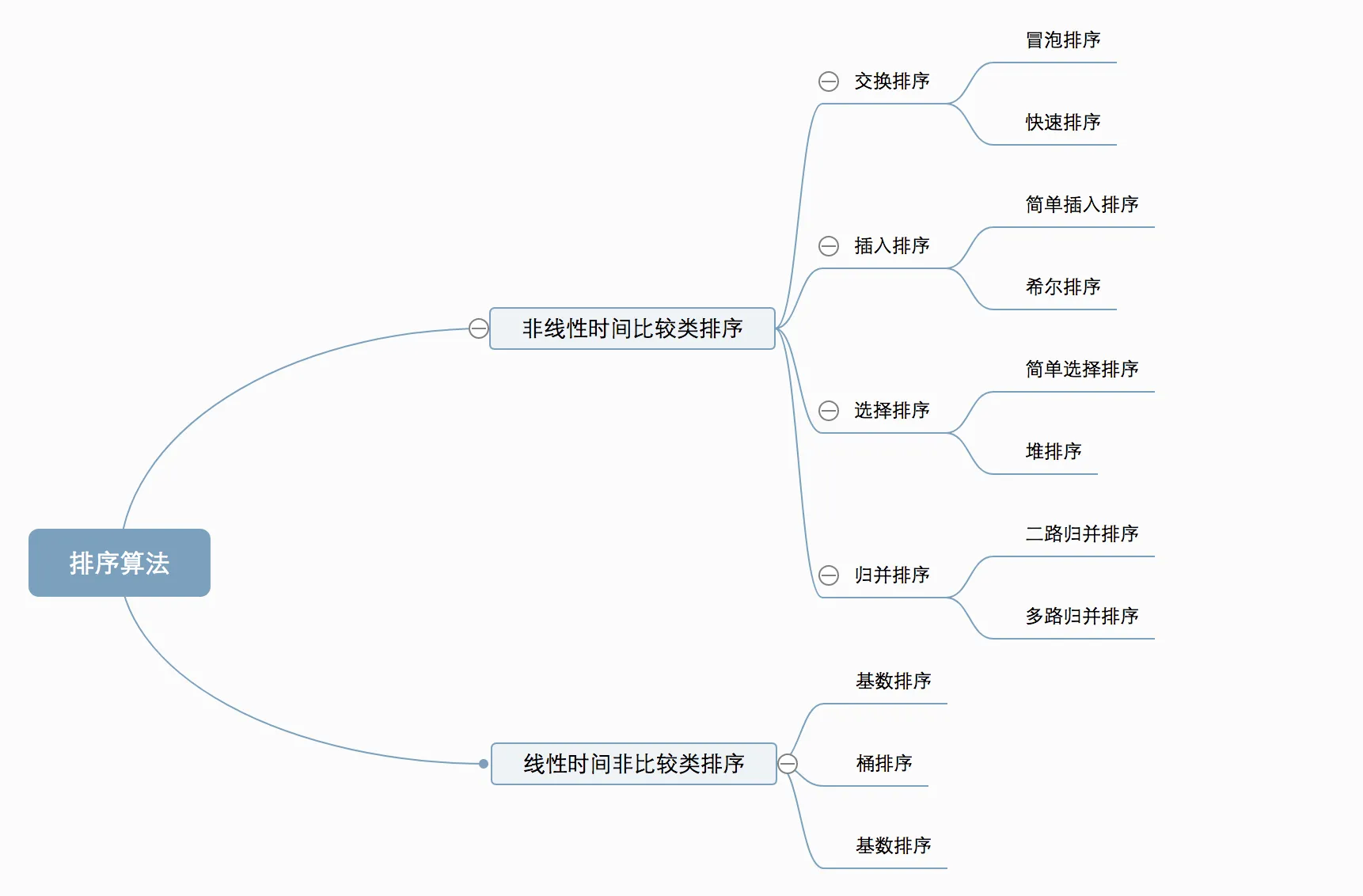
The 10 classic sorting algorithms can be divided into two main categories:

Non-linear time comparison-based sorting: These algorithms determine the relative order of elements by comparing them. Since their time complexity cannot break through $O(n log n)$, they are called non-linear time comparison-based sorting algorithms.

Linear time non-comparison-based sorting: These algorithms do not determine the relative order of elements by comparison. They can break through the lower bound of comparison-based sorting and run in linear time, hence they are called linear time non-comparison-based sorting algorithms.

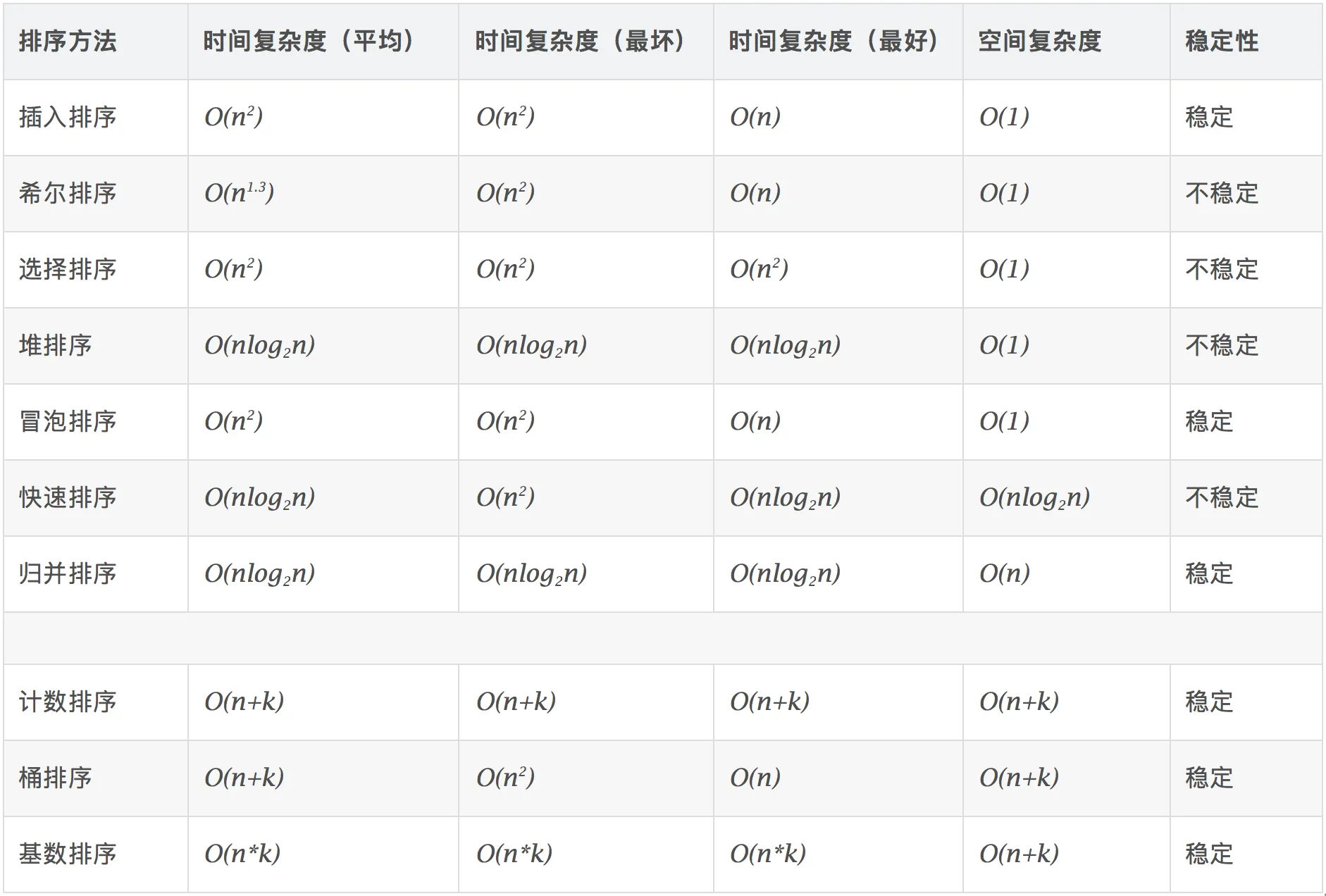
Their time and space complexity are:

Below is a detailed introduction to each sorting algorithm and its Python implementation.

1. Bubble Sort

Bubble sort is a simple sorting algorithm. It repeatedly steps through the list, compares adjacent elements, and swaps them if they are in the wrong order. This process is repeated until no swaps are needed, indicating that the list is sorted. The algorithm gets its name because smaller elements gradually “bubble” to the top of the list through exchanges, like bubbles in water.

1.1 Algorithm Description

• Compare adjacent elements. If the first is greater than the second, swap them.
• Repeat this process for each pair of adjacent elements, from the beginning to the end of the list. After the first pass, the largest element will be at the end.
• Repeat the above steps for all elements, excluding the last one (which is already in its correct place).
• Continue repeating these steps until no swaps occur, which means the array is sorted.

1.2 Animated Demonstration

1.3 Python3 Code Implementation

    import numpy as np
    import random

    def bubble_sort(ownlist):
        n = len(ownlist)

        # Traverse through all array elements
        for i in range(n):

            # Last i elements are already in place
            for j in range(0, n-i-1):

                # traverse the array from 0 to n-i-1
                # Swap if the element found is greater
                # than the next element
                if ownlist[j] > ownlist[j+1] :
                    ownlist[j], ownlist[j+1] = ownlist[j+1], ownlist[j]
            print(ownlist)

    a = random.sample(list(np.arange(100)),20)
    bubble_sort(a)

2. Selection Sort

Selection sort is a simple and intuitive sorting algorithm. Its working principle is as follows: first, find the minimum (or maximum) element in the unsorted portion of the list and place it at the beginning of the sorted portion. Then, continue to find the minimum (or maximum) element from the remaining unsorted elements and append it to the end of the sorted portion. This process repeats until all elements are sorted.

2.1 Algorithm Description

A direct selection sort for $n$ records can obtain an ordered result after $n-1$ passes of direct selection sort.

• Initial state: The unsorted region is $[1..n]$, and the sorted region is empty.
• $i$-th pass ($i=1,2,3…n-1$): At the beginning of the $i$-th pass, the current sorted region and unsorted region are $R[1..i-1]$ and $R(i..n)$ respectively. In this pass, select the record $R[k]$ with the smallest key from the current unsorted region, and swap it with the first record in the unsorted region. This makes $R[1..i]$ a new sorted region with one more record, and $R[i+1..n)$ a new unsorted region with one less record.
• The array becomes ordered after $n-1$ loops.

2.2 Animated Demonstration

2.3 Python3 Code Implementation

    import numpy as np
    import random

    def selection_sort(ownlist):
        n = len(ownlist)

        for i in range(n):

            minn = i
            for j in range(i, n):

                if ownlist[j] < ownlist[minn] :
                    minn = j
            if minn!=i:
                ownlist[i],ownlist[minn] = ownlist[minn],ownlist[i]
            print(ownlist)

    a = random.sample(list(np.arange(100)),20)
    selection_sort(a)

3. Insertion Sort

Insertion Sort is a simple and intuitive sorting algorithm. Its working principle involves building a sorted sequence one element at a time. For unsorted data, it scans backward from the end of the sorted sequence, finds the appropriate position, and inserts the new element.

3.1 Algorithm Description

1. Start with the first element; it can be considered already sorted.
2. Take the next element, and scan backward through the already sorted sequence. If a sorted element is greater than the new element, shift that sorted element to the next position. Repeat until you find a sorted element that is less than or equal to the new element’s value. Insert the new element at that position.
3. Repeat step 2 until all elements are sorted.

3.2 Animated Demonstration

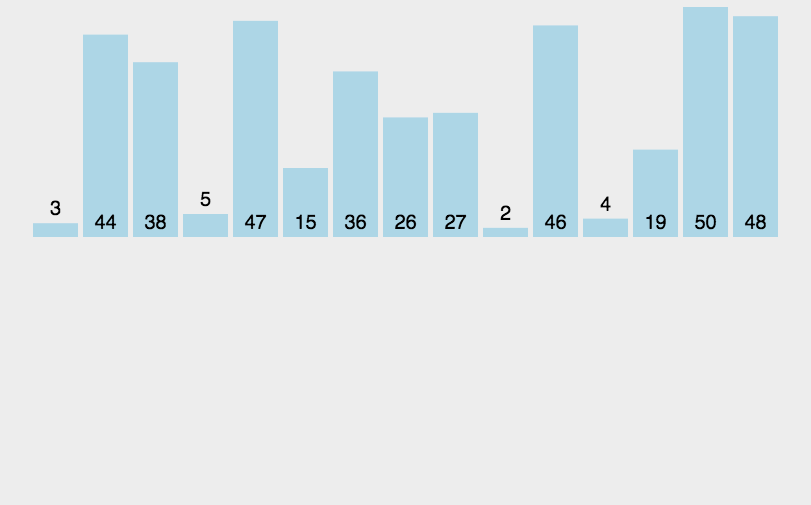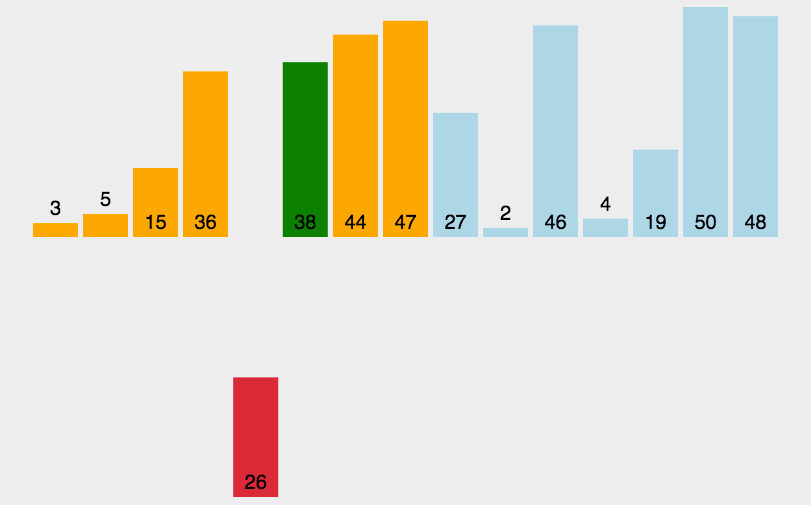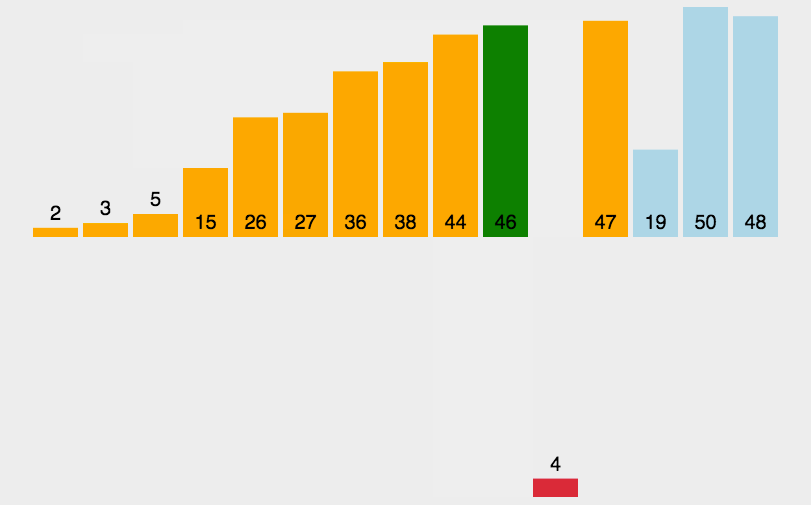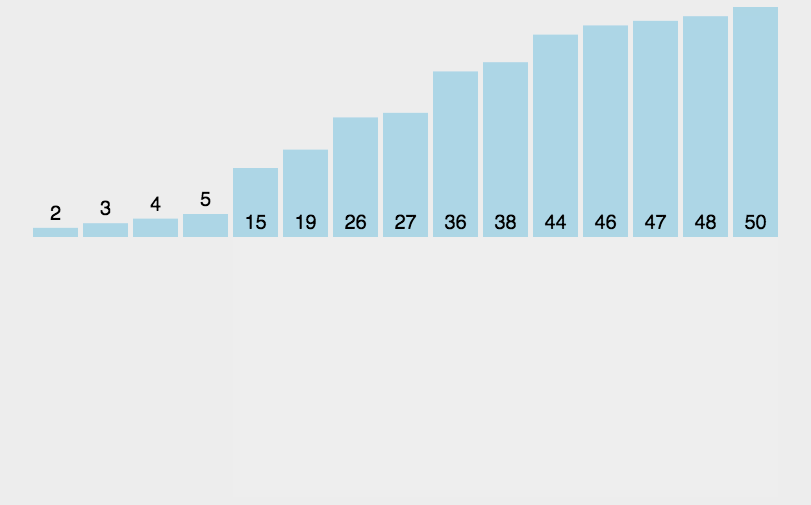
3.3 Python3 Code Implementation

    import numpy as np
    import random
    def insertion_sort(ownlist):
        for index in range(1,len(ownlist)):

            currentvalue = ownlist[index]
            position = index

            while position>0 and ownlist[position-1]>currentvalue:
                ownlist[position]=ownlist[position-1]
                position = position-1

            ownlist[position]=currentvalue
            print(ownlist)
    a = random.sample(list(np.arange(100)),20)
    insertion_sort(a)

4. Shell Sort

Shell Sort, also known as diminishing increment sort, is a more efficient improved version of insertion sort. Shell sort is an unstable sorting algorithm. Shell sort proposes an improvement based on the following two properties of insertion sort: insertion sort is efficient when operating on almost sorted data, achieving linear sorting efficiency. However, insertion sort is generally inefficient because it can only move data one position at a time.

4.1 Algorithm Description

First, divide the entire sequence of records to be sorted into several sub-sequences and perform direct insertion sort on each. The specific algorithm description is:

• Choose an increment sequence $t_1, t_2, ldots, t_k$, where $t_i > t_j$ and $t_k=1$.
• Perform $k$ passes of sorting based on the number of increments.
• In each pass, according to the corresponding increment $t_i$, divide the sequence to be sorted into several sub-sequences of length $m$. Perform direct insertion sort on each sub-list. Only when the increment factor is 1, the entire sequence is treated as one list, and the list length is the length of the entire sequence.

4.2 Animated Demonstration

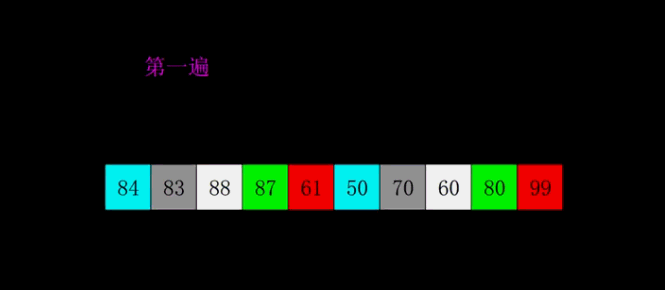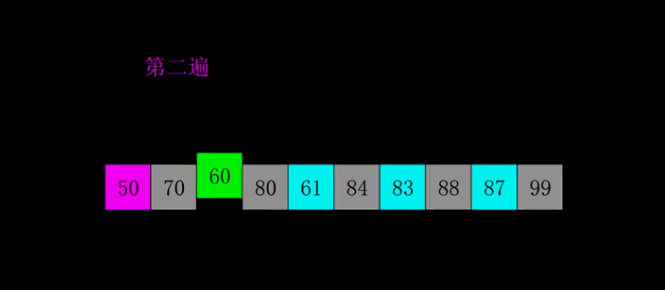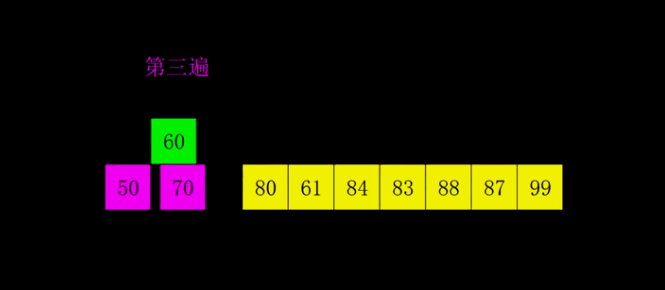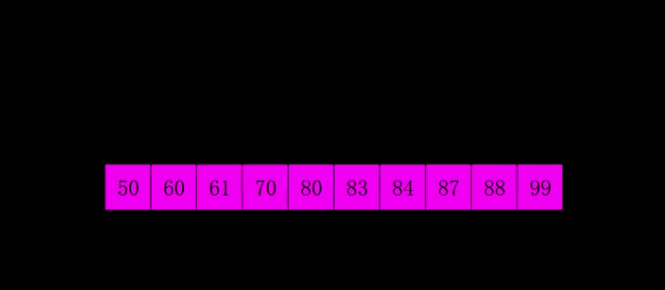
4.3 Python3 Code Implementation

    import numpy as np
    import random
    def shell_sort(ownlist): 

        n = len(ownlist) 
        gap = n//2
        while gap > 0: 

            for i in range(gap,n): 

                temp = ownlist[i] 

                j = i 
                while  j >= gap and ownlist[j-gap] >temp: 
                    ownlist[j] = ownlist[j-gap] 
                    j -= gap 

                ownlist[j] = temp 
            gap //= 2
            print(ownlist)
    a = random.sample(list(np.arange(100)),20)
    print(a)
    shell_sort(a)

5. Merge Sort

Merge Sort is an efficient sorting algorithm based on the merge operation. This algorithm is a very typical application of the divide and conquer strategy. It merges already sorted sub-sequences to obtain a fully sorted sequence; that is, it first sorts each sub-sequence and then sorts the elements between the sub-sequences. If two sorted lists are merged into one sorted list, it is called a 2-way merge.

5.1 Algorithm Description

• Divide the input sequence of length $n$ into two sub-sequences of length $n/2$.
• Recursively apply merge sort to these two sub-sequences.
• Merge the two sorted sub-sequences into one final sorted sequence.

5.2 Animated Demonstration

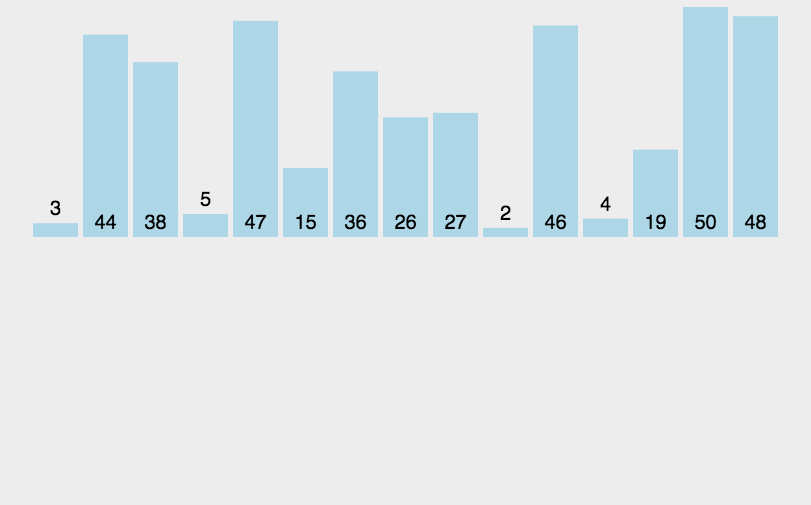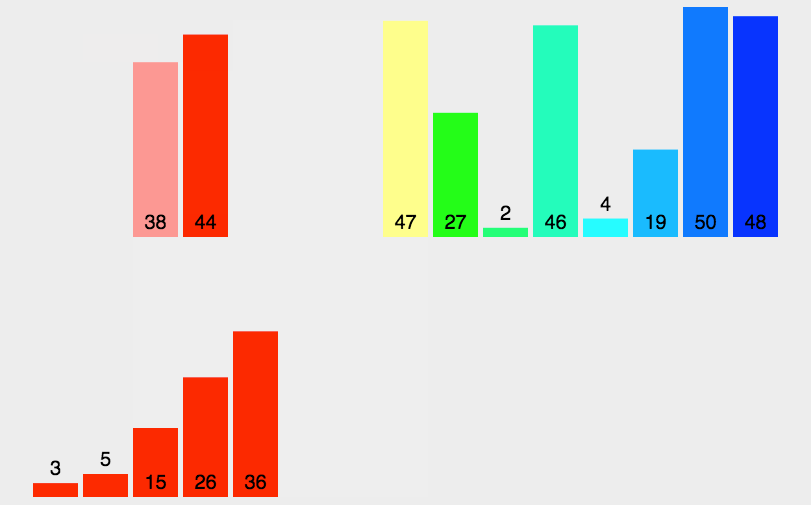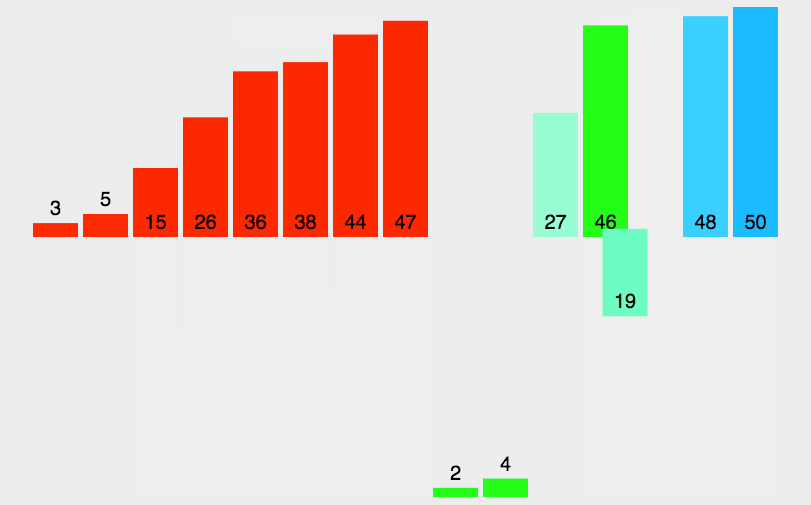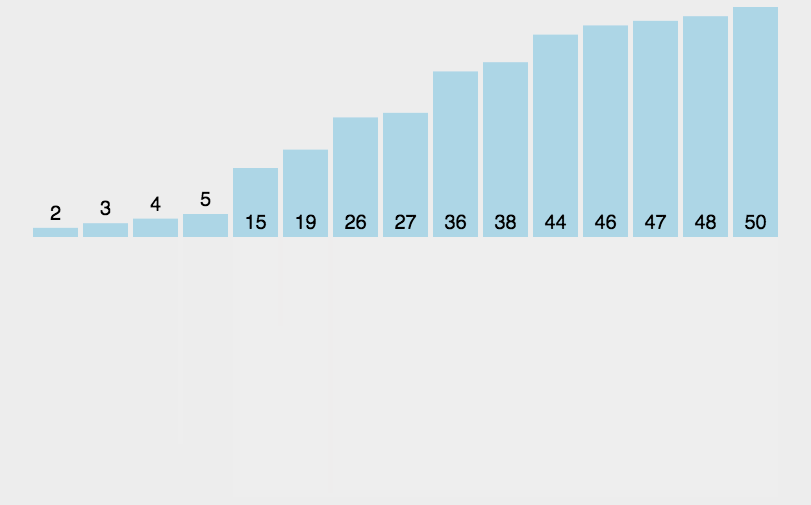
5.3 Python3 Code Implementation

    import numpy as np
    import random
    def merge_sort(ownlist):
        print("Split ",ownlist)
        if len(ownlist)>1:
            mid = len(ownlist)//2
            lefthalf = ownlist[:mid]
            righthalf = ownlist[mid:]

            merge_sort(lefthalf)
            merge_sort(righthalf)

            i=0 #left
            j=0 #right
            k=0 #
            while i < len(lefthalf) and j < len(righthalf):
                if lefthalf[i] < righthalf[j]:
                    ownlist[k]=lefthalf[i]
                    i=i+1
                else:
                    ownlist[k]=righthalf[j]
                    j=j+1
                k=k+1

            while i < len(lefthalf):
                ownlist[k]=lefthalf[i]
                i=i+1
                k=k+1

            while j < len(righthalf):
                ownlist[k]=righthalf[j]
                j=j+1
                k=k+1
        print("Merging ",ownlist)
    a = random.sample(list(np.arange(100)),20)
    print(a)
    merge_sort(a)

Summary:

This article introduced the principles of 5 sorting algorithms and their Python 3 implementations. The next article will delve into the remaining algorithms: Quick Sort, Heap Sort, Counting Sort, Bucket Sort, and Radix Sort, along with their Python 3 implementation code.