While solving LeetCode problems, I encountered a question about finding the longest palindromic substring.
The official solutions provide four methods:
- Brute Force
- Dynamic Programming
- Center Expansion Algorithm
- The Manacher method, which we will introduce today.
Before introducing the algorithm, let’s first define what a palindrome is. Simply put, a palindrome is a string that reads the same forwards and backwards, such as “aba”, “上海自来水来自海上” (Shanghai tap water comes from the sea), etc. The longest palindromic substring of a given string is the longest substring of that string that is also a palindrome.
Manacher’s algorithm is the most efficient, with a time complexity of O(n).
Manacher Algorithm Principle and Implementation
Manacher’s algorithm provides a clever way to handle palindromes of both odd and even lengths. The specific approach is to insert a delimiter ‘#’ between every two characters in the original string, and also insert ‘(@)’ at the beginning and a delimiter (’$’) at the end.
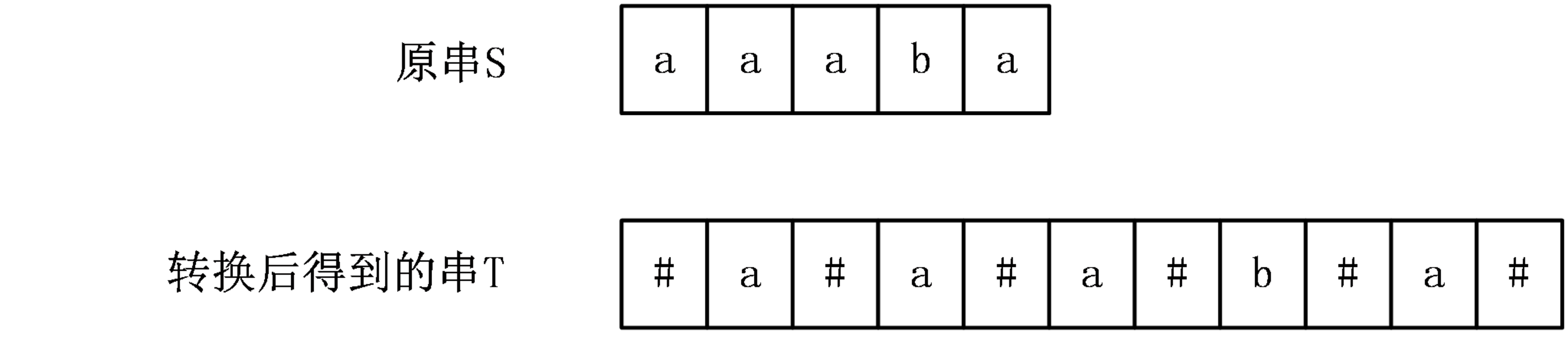
Calculating the Len Array
Calculate Len[i] from left to right. When calculating Len[i], Len[j] (where 0 <= j < i) has already been calculated. Let P be the maximum right endpoint of the longest palindromic substring calculated so far, and let po be the position where this maximum value was achieved. There are two cases:
Case 1: i <= P
Find the symmetric position of i with respect to po, let’s call it j. If Len[j] < P - i:
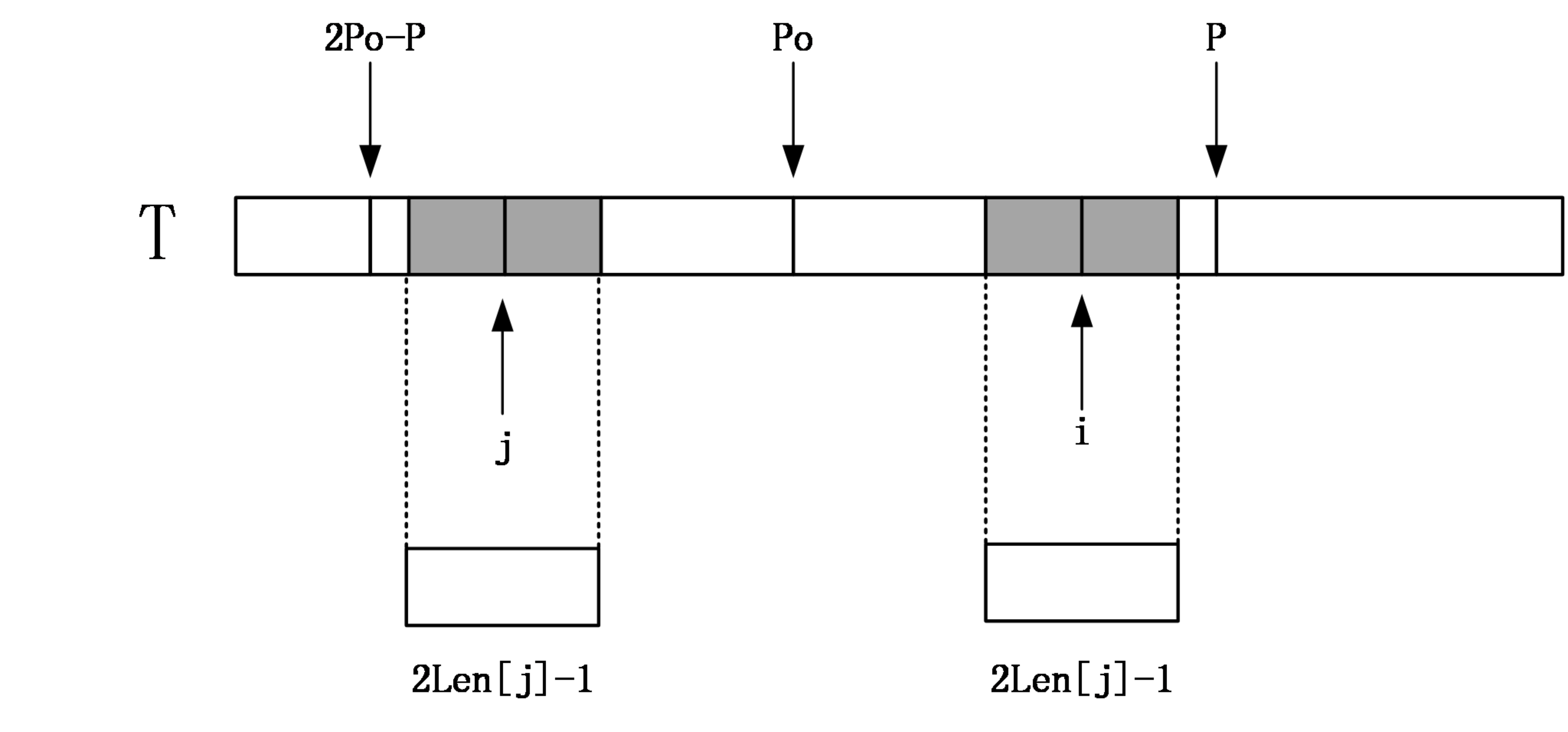
This means that the palindrome centered at j is entirely within the palindrome centered at po. Since j and i are symmetric with respect to po, and by the definition of a palindrome, a palindrome read backwards is still a palindrome, the length of the palindrome centered at i is at least the same as the palindrome centered at j, i.e., Len[i] >= Len[j]. Because Len[j] < P - i, it implies i + Len[j] < P. By symmetry, we know Len[i] = Len[j].
If Len[j] >= P - i, by symmetry, this means the palindrome centered at i might extend beyond P. The portion beyond P has not yet been matched, so we must start matching one by one from position P+1 until a mismatch occurs. This process will then update P, the corresponding po, and Len[i].
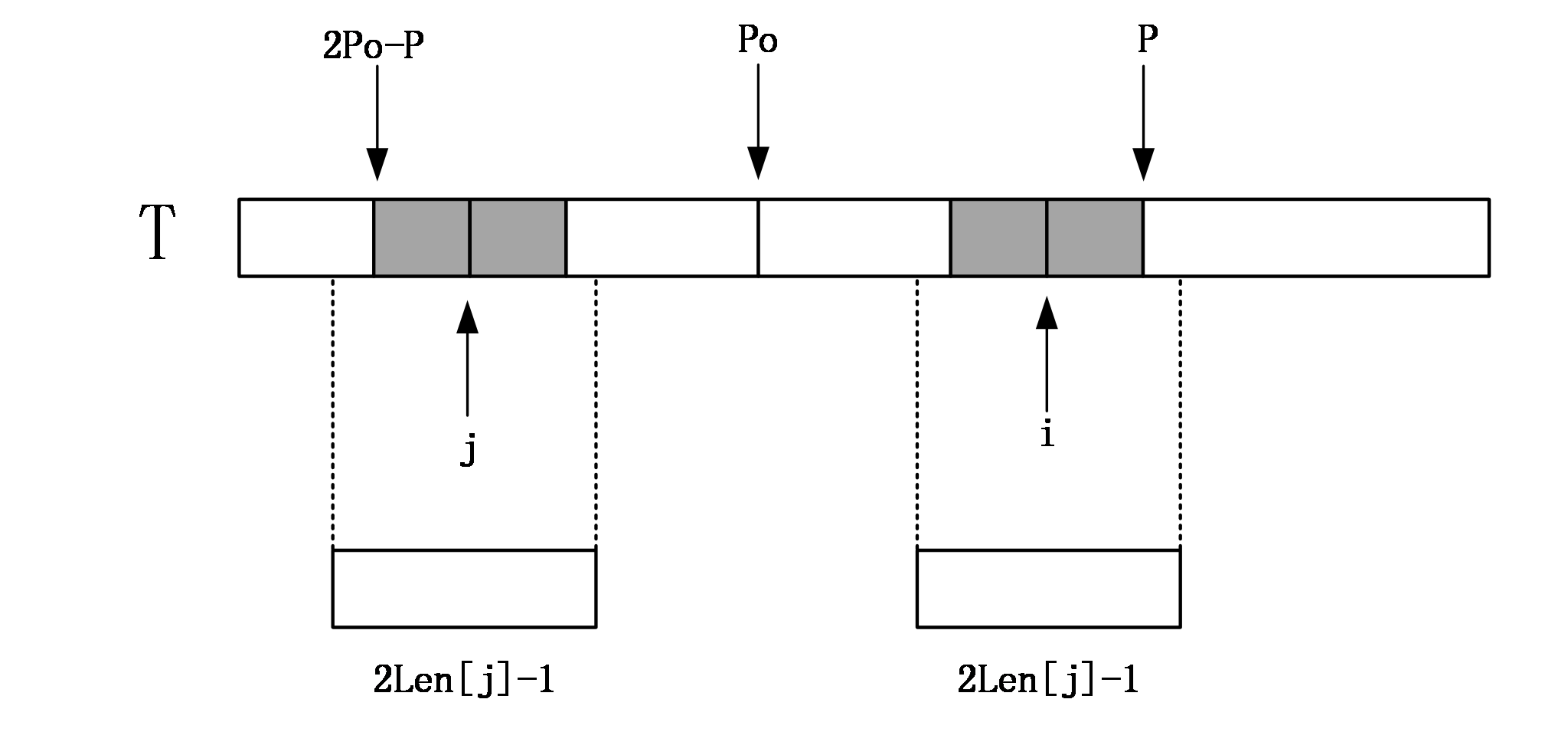
Case 2: i > P
If i is greater than P, it means that no part of the palindrome centered at i has been matched yet. In this situation, we can only proceed by matching characters one by one. After the matching is complete, P, the corresponding po, and Len[i] must be updated.
Python3 Implementation of Manacher Algorithm
def longestPalindrome(self, s: str) -> str:
s = "@#"+"#".join(s)+"#$"
mx,ans,p0=0,0,0 ##### Rightmost position, maximum length, center position
Len = [0]*len(s)
mxstr = ''
for i in range(len(s)):
if mx>i:
Len[i]=min(mx-i,Len[2*p0 - i])
else:
Len[i] = 1
while i+Len[i]<len(s) and s[i-Len[i]]==s[i+Len[i]]:
Len[i] += 1
if Len[i]+i > mx :
mx=Len[i]+i
p0 = i
if Len[i] >= ans:
mxstr = s[i-Len[i]+1:i+Len[i]]
ans=Len[i]
return mxstr.replace("#","").replace("$","")
