When dealing with high-dimensional single datasets, techniques like LDA and PCA can be used for dimensionality reduction. However, if two datasets come from the same set of samples but differ significantly in type and scale, what can we do? This is where Canonical Correlation Analysis (CCA) comes in. CCA allows us to analyze two datasets simultaneously. Typical applications include joint analyses in biology such as transcriptomics and proteomics, metabolomics, or microbiome studies. For more, see Wikipedia.
Relationship and Differences Between CCA and PCA
CCA is somewhat similar to PCA (Principal Component Analysis). Both were introduced by the same research group and can be thought of as dimensionality reduction techniques.
However:
- PCA aims to find linear combinations of variables within one dataset that explain the most variance.
- CCA aims to find linear combinations between two datasets that explain the maximum correlation.
Python Implementation of CCA
How do we implement CCA in Python?
The sklearn.cross_decomposition module provides the CCA function. Let’s take the penguins dataset as an example.
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
filename = "penguins.csv"
df = pd.read_csv(filename)
df = df.dropna()
df.head()
Sample data looks like:
species island bill_length_mm bill_depth_mm flipper_length_mm body_mass_g sex
0 Adelie Torgersen 39.1 18.7 181.0 3750.0 MALE
1 Adelie Torgersen 39.5 17.4 186.0 3800.0 FEMALE
2 Adelie Torgersen 40.3 18.0 195.0 3250.0 FEMALE
4 Adelie Torgersen 36.7 19.3 193.0 3450.0 FEMALE
5 Adelie Torgersen 39.3 20.6 190.0 3650.0 MALE
We select two sets of features:
- Group 1:
bill_length_mm,bill_depth_mm - Group 2:
flipper_length_mm,body_mass_g
from sklearn.preprocessing import StandardScaler
df1 = df[["bill_length_mm","bill_depth_mm"]]
df1_std = pd.DataFrame(StandardScaler().fit(df1).transform(df1), columns = df1.columns)
df2 = df[["flipper_length_mm","body_mass_g"]]
df2_std = pd.DataFrame(StandardScaler().fit(df2).transform(df2), columns = df2.columns)
Sample output:
# df1_std
bill_length_mm bill_depth_mm
-0.896042 0.780732
-0.822788 0.119584
-0.676280 0.424729
-1.335566 1.085877
-0.859415 1.747026
# df2_std
flipper_length_mm body_mass_g
-1.426752 -0.568475
-1.069474 -0.506286
-0.426373 -1.190361
-0.569284 -0.941606
-0.783651 -0.692852
Now we perform CCA:
from sklearn.cross_decomposition import CCA
ca = CCA()
xc, yc = ca.fit(df1, df2).transform(df1, df2)
Check output shapes:
np.shape(xc) # (333, 2)
np.shape(yc) # (333, 2)
Check correlation:
np.corrcoef(xc[:, 0], yc[:, 0])
np.corrcoef(xc[:, 1], yc[:, 1])
Output:
array([[1. , 0.78763151],
[0.78763151, 1. ]])
array([[1. , 0.08638695],
[0.08638695, 1. ]])
Now combine CCA results with species and sex for visualization:
cca_res = pd.DataFrame({
"CCA1_1": xc[:, 0],
"CCA2_1": yc[:, 0],
"CCA1_2": xc[:, 1],
"CCA2_2": yc[:, 1],
"Species": df.species,
"sex": df.sex
})
cca_res.head()
CCA1_1 CCA2_1 CCA1_2 CCA2_2 Species sex
-1.186252 -1.408795 -0.010367 0.682866 Adelie MALE
-0.709573 -1.053857 -0.456036 0.429879 Adelie FEMALE
-0.790732 -0.393550 -0.130809 -0.839620 Adelie FEMALE
-1.718663 -0.542888 -0.073623 -0.458571 Adelie FEMALE
-1.772295 -0.763548 0.736248 -0.014204 Adelie MALE
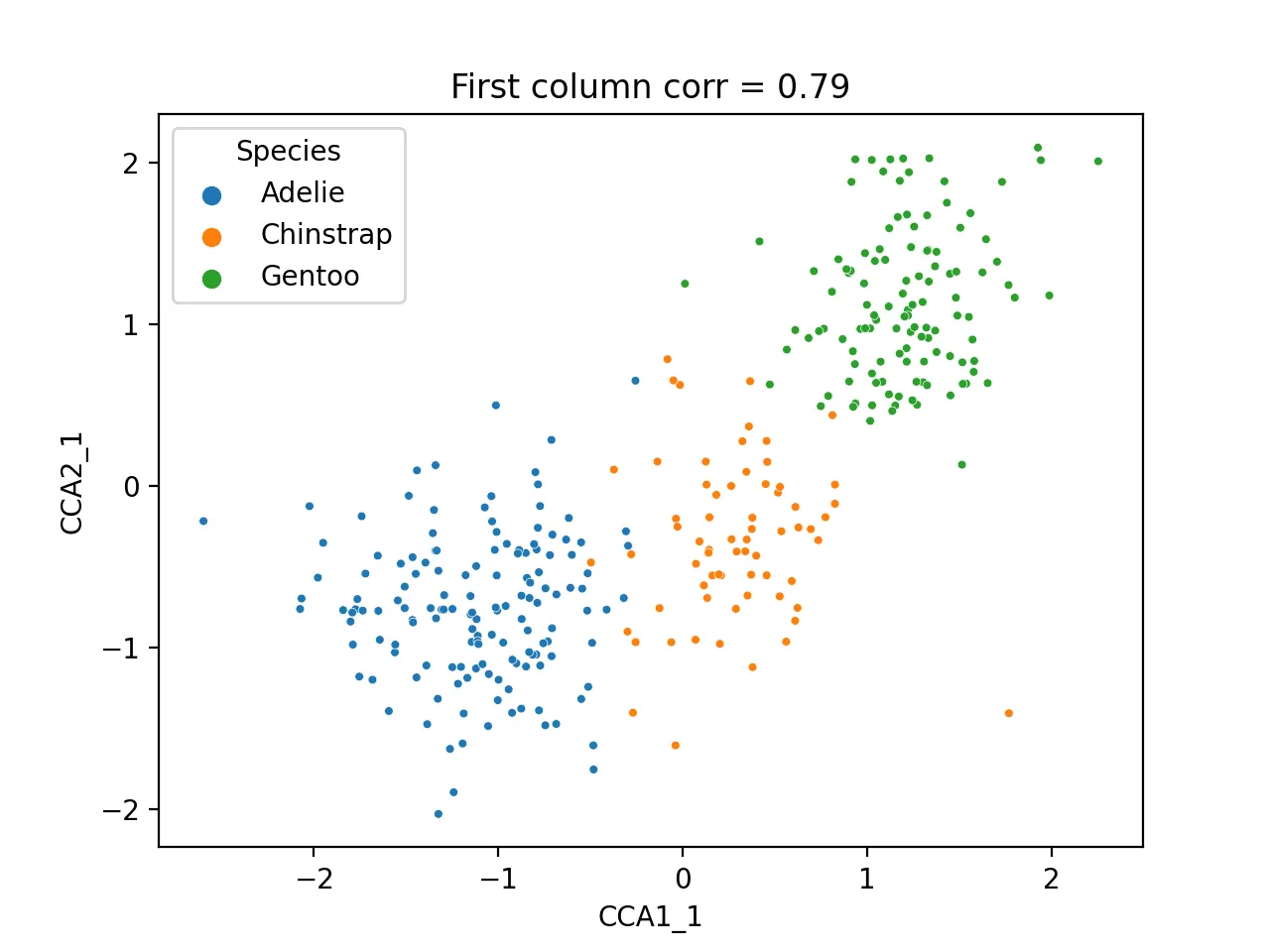
Scatter plot of first CCA component:
sns.scatterplot(data=cca_res, x="CCA1_1", y="CCA2_1", hue="Species", s=10)
plt.title(f'First column corr = {np.corrcoef(cca_res.CCA1_1, cca_res.CCA2_1)[0, 1]:.2f}')
plt.savefig("cca_first.png", dpi=200)
plt.close()
Heatmap of correlation between CCA results and original metadata:
cca_df = pd.DataFrame({
"cca1_1": cca_res.CCA1_1,
"cca1_2": cca_res.CCA1_2,
"cca2_1": cca_res.CCA2_1,
"cca2_2": cca_res.CCA2_2,
"Species": df.species.astype('category').cat.codes,
"Island": df.island.astype('category').cat.codes,
"sex": df.sex.astype('category').cat.codes
})
dfcor = cca_df.corr()
mask = np.triu(np.ones_like(dfcor))
sns.heatmap(dfcor, cmap="bwr", annot=True)
plt.savefig("cca_corr.png", dpi=200)
plt.close()
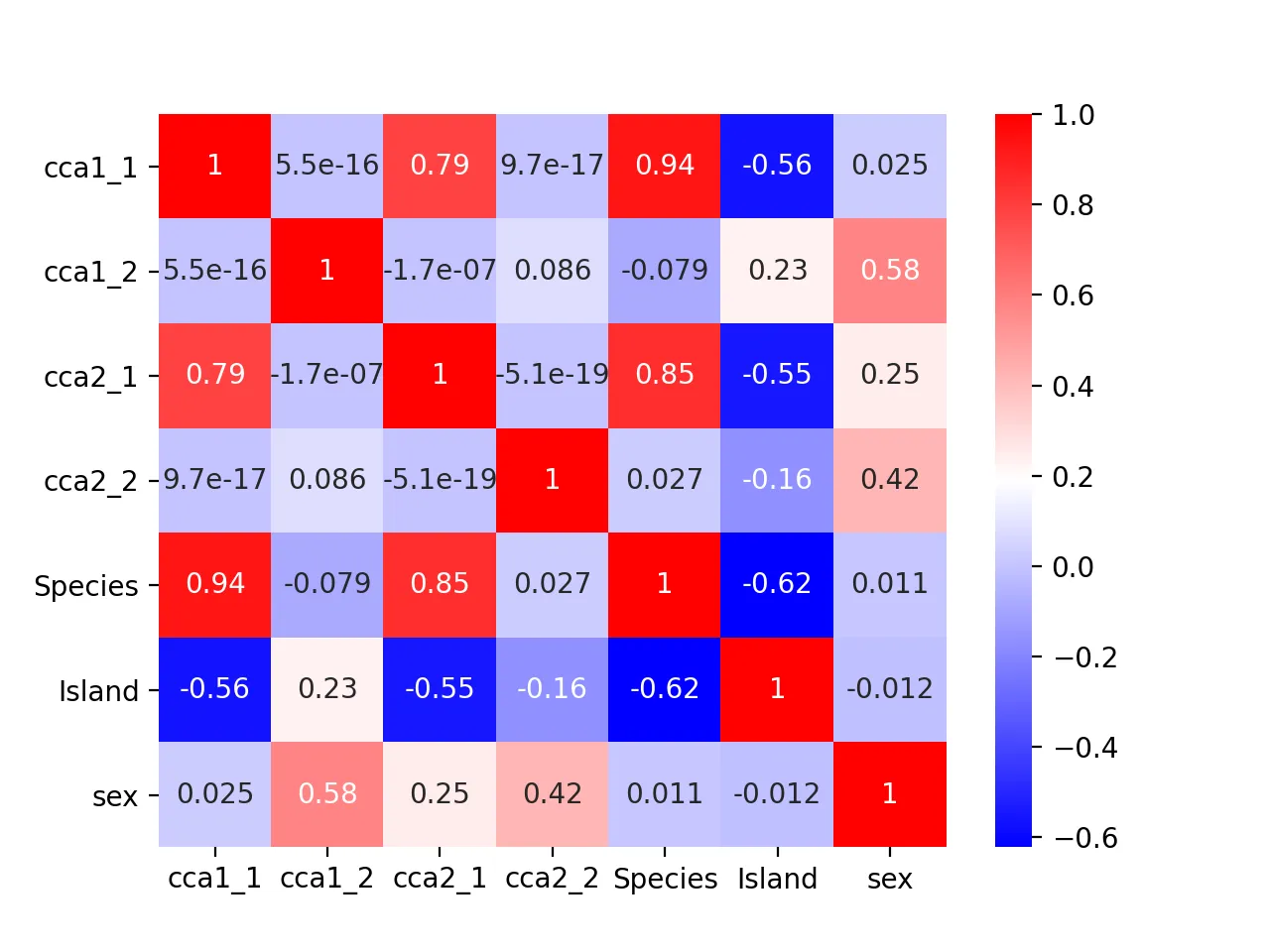
It turns out that the second pair of canonical variables correlates most with sex (correlation = 0.42), indicating it may encode sex information.
sns.scatterplot(data=cca_res, x="CCA1_2", y="CCA2_2", hue="sex", s=10)
plt.title(f'Second column corr = {np.corrcoef(cca_res.CCA1_2, cca_res.CCA2_2)[0, 1]:.2f}')
plt.savefig("cca_sex.png", dpi=200)
plt.close()
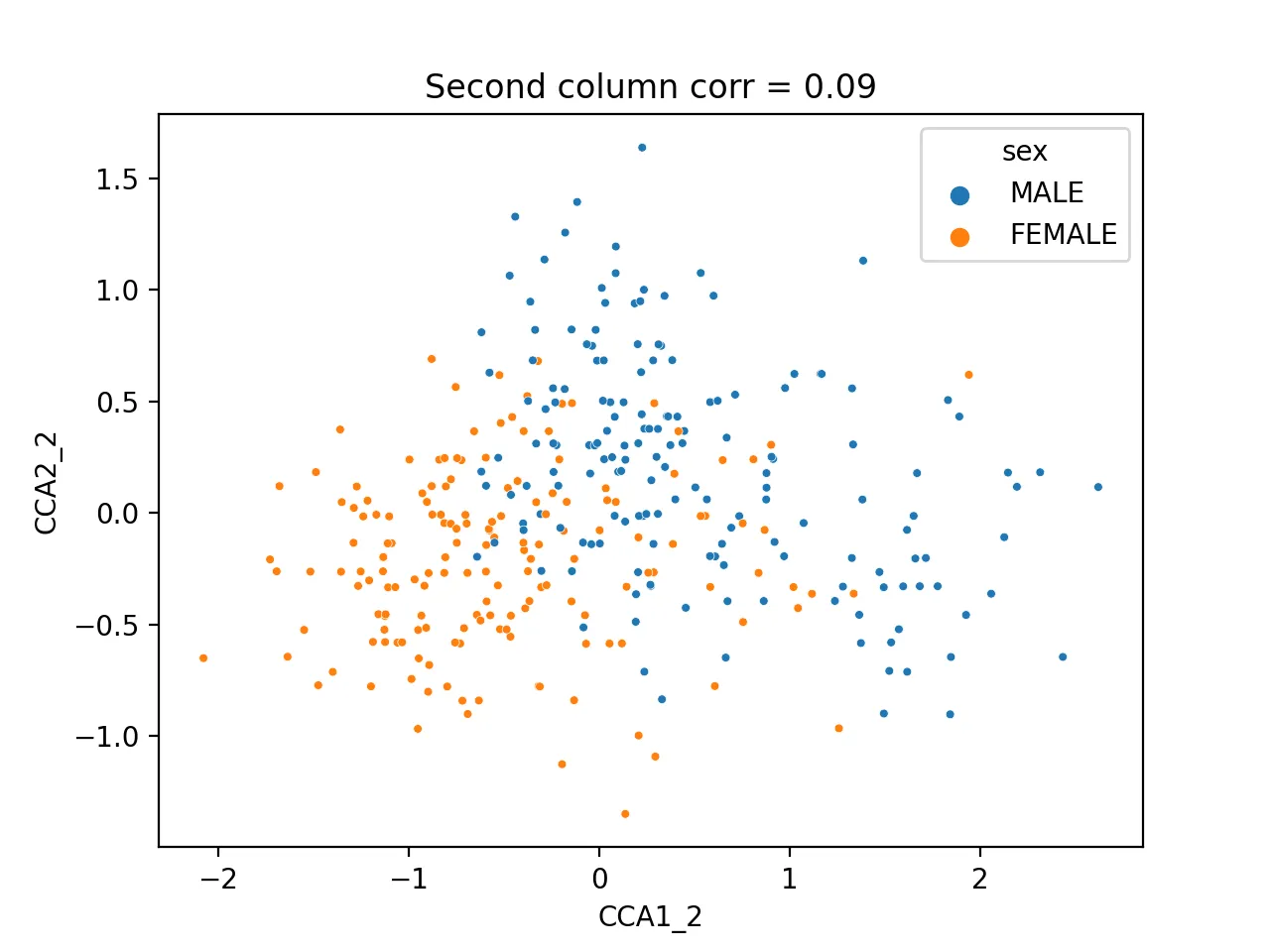
Different sexes are clearly separable.
Summary
CCA is an effective method for jointly analyzing multi-type datasets in high-dimensional spaces. It performs well on the penguin dataset and is a foundational tool in multi-omics analysis in biology. In future posts, we’ll explore more multi-omics integration methods.
